Tech Stuff - Equalization (EQ), Metering and the FFT

One of the most powerful techniques for manipulation of audio, both in the analog and digital domain, is equalization (EQ), both when mixing multiple inputs to create an audio output or when playing existing audio material. Equalization allows all kinds of magic such as the ability to pull out voice from the background, accentuate the bass, suppress a particularly noisy instrument or clip tinny sounding higher frequencies. But in order to work the magic you need to know frequencies the things you want to accentuate (or suppress) occupy as well as their harmonic characteristics.

Once you have mastered those minor (irony warning) details the real fun of equalization can begin. This page collects information about software based equalization (though most principles remain the same for analog hardware solutions) and its related cousin - frequency analysis.

Serious Confusion Warning: Most equalizers, especially band equalizers, use the terms Octave , 1/3 Octave, 1/12 Octave etc. This use should not be confused with a musical Octave. A musical Octave has a frequency range from C to B based on a reference (tuning) frequency of A4 = 440 Hz. Equalizer Octaves are normally based on a reference frequency of 1000 Hz (1 KHz - the ISO and ANSI standard). Both types of octave have the standard Octave property of a 2:1 ratio, thus moving from one octave to the next will result in a doubling of the frequency. The term Decade is sometimes used in equalization meaning a 10:1 ratio between the decades (normally 20 Hz to 200 Hz, 200 - 2Khz, 2KHz to 20 Khz). Finally, like much in the audio world most terms have their roots in the analog world - when applied to digital systems many terms are either not meaningful or may have very different properties.

Equalization - Overview

An equalizer allows boosting (or suppression/attenuation) of frequencies between the source of a sound (a microphone or recorded material) and the output of the sound (a loudspeaker system or recording system). Equalizers normally work on groups of frequencies called frequency bands or more commonly just bands. Analog equalizers come in all shapes and sizes with the most common today being what is called a graphic equalizer - a big board with lots of slider controls for individual bands. This page focuses on software based equalizers for manipulating recorded (digital) audio but most of the principles remain the same. First, some categorization:

Simple: An equalizer which attempts to fulfil some end-user driven function and as such tends to have simplistic effect labeling. It is typified by the 2 band (normally labelled Bass and Treble) and the 3 band equalizer, normally labeled Bass, Mid and Treble which is based on 3 decades (10:1 ratios) of 20Hz - 200Hz (Bass), 200Hz - 2 KHz (Mid) and 2KHz to 20 KHz (treble). Controls are usually software sliders or knobs mimicking their real world counterparts. These equalizers have fixed functionality (or presets) and rarely come with any documentation describing the frequencies being affected. Boost (gain) or suppressing (attenuation) scales tend to be limited to + and -. More feature rich simple equalizers will label the effects, for example, iTunes use of Vocal Booster, Dance etc.. Use of these equalizers requires an act of faith in assuming that the designers/developers selected sensible frequency ranges. Nothing wrong with a simple equalizer if you get the the desired result.
Band Equalizers: These equalizers control specific frequency bands and allow fine-grained control over the gain (boost) or suppression (attenuation) within the bands. Gain/Attenuation ranges will vary from +-6 dB to +-24 dB or even greater. The frequency bands cover the full audio range of 20Hz to 20Khz and are typically based on an Octave (9 to 11 bands), 2/3 octave (15 - 17 bands) and 1/3 octave (30 - 31 bands) being the most common. (Note: There are also 17 - 22 band equalizers which may be 1/2 octave or use frequency ranges defined by the supplier). With modern software 1/6, 1/12 and 1/24 octave or even higher equalizers are possible but require some serious thought about the user interface since a 1/24 octave equalizer covering the entire audible region would have more than 200 bands to control! Equalizers that support bands lower than an Octave are frequently called Fractional Octave Equalizers. Most band equalizers label their frequency bands according to the ISO Preferred Frequency standard (ISO 266:1997 or ANSI equivalent S1.6-1984) and use appropriate standard methods for calculation of band centers. The Preferred Frequency specification contains both a Preferred Frequency value and a Calculated Center value. Either may be used according to the desired accuracy.
Harmonic Equalizers: The term is relatively new to acoustics and historically was typically used to describe power and optic rectification systems. In principle the term can be applied to acoustic equalizers having similar properties to band equalizers but which allow the user to control the harmonics (and overtones) using some form of sound specific, say, a musical instrument, profile describing the harmonic relationships. If a band is boosted and the profile is, say, a piano, then the corresponding harmonic (and overtone) frequencies can be boosted (or attenuated) automatically by some proportion based on the instrument's harmonic profile and the detected audio material. Thus if, say, the band 250Hz is boosted by 10dB and C4 (262Hz) is detected in the audio stream then the 2nd harmonic (at 524 Hz) would be boosted by, say, 30% or to a 30% level relative to the adjusted fundamental.
Enhancement: These equalizers have similar properties to harmonic equalizers but allow the user to add harmonic (and overtone) material based on some form of, typically, instrument profile. If a band is boosted and the profile is, say, a saxophone then the corresponding harmonic (and overtone) frequencies are added (if necessary) automatically to some proportion of the fundamental tone based on the profile and the detected audio material. Thus if, say, the band 250Hz is boosted by 10dB and C4 (262Hz) is detected in the audio stream then the 2nd harmonic (at 524 Hz) would be added (if required) or boosted to make it, say, 30% relative to the fundamental and so on through the various harmonics. Enhancers are clearly controversial since they can add audio material which was not present in the captured recording, whereas classic equalizers merely manipulate material that exists in the audio stream.

Preferred and Calculated Center Frequencies

ISO band equalizers normally allocate (and label) the bands based on the ISO Preferred Frequencies (defined in ISO R 266-1997 or ANSI equivalent S1.6-1984). Center frequencies may be Preferred or Calculated (the later occasionally referred to, somewhat misleadingly, as Exact Centers). The Calculated centers for each band are computed, starting from a base frequency of 1,000 Hz, using one of two (base 10 and base 2) standard algorithms and the resulting frequency value is compared with a table of Preferred values to find the closest Preferred frequency match. The tables are Renard number series known as R5, R10, R20, R40 or R80 and defined in the ISO/ANSI standard. A specific table is used depending on the fractional octave value, for example, R20 is used when the fractional octave is either 1/6 or 1/2 and R40 is used for 1/12 octaves. At one level the Preferred value is simply a convenience for simple mortals since it is typically a nice rounded value but at another level can, at the users discretion, be used for all subsequent computations. Much of the literature suggests that only the Calculated centers should be used for this purpose. This is not what the standards say. They allow either center to be used. However, the standards also say that if serious (up to 5 decimal place) computation is being performed this should be done using the Calculated values. Clearly the centers (Preferred or Calculated) defined are centers of a frequency band. The standards, however, appear entirely silent on the topic of edge/crossover band frequencies and their calculation which seems, on its face, a bit of an overight.

Equalization strategies within the bands can vary significantly. The band can be uniformly boosted across its frequency range which can lead to abrupt changes in the adjacent bands. Alternatively, the center of the band can be boosted to the full gain and attenuated toward both edges which can result in very peaky equalization. Perhaps with historic analog equipment these were the best possible outcomes. Digital techniques can bring a totally different set of control functions from the simplest which takes into account adjacent settings, through harmonic profiles, to perhaps automatic equalizers which can react in real time according to a given set of parameters describing what to do at different frequencies and dB levels. Figure 1 crudely illustrates some possible strategies:

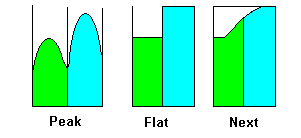
Figure 1 - EQ Strategies for Adjacent Bands

The strategy labeled Next seeks to take into account neighbouring band EQ values and build attenuation/boost characteristics within the bands to ensure a smooth transition between bands. Such a strategy is only really possible in a digital equalizer whereas the Peak and Flat strategies are possible with either an analog or a digital equalizer.

Frequency Bands

ISO R 266-1997 (and equivalent ANSI S1.6-1984) defines the Preferred Frequencies (and a convenience Band number), their associated band range and center frequency based on a starting point of 1000 Hz (1 KHz). The term Preferred Frequency simply refers to a convenient label for we limited humans to work with whereas the term Center Frequency is a precise value which is used for all computations. Thus, for example, Band 12 has a Preferred Frequency (a label or sometimes referred to as the Nominal Center Frequency) of 16Hz but a computed Center Frequency (sometimes referred to as the Exact Center) of 15.85 Hz.

Warning: If this stuff is vitally important the source documents should always be consulted directly (and require that you pay handsomely for the privilege of doing so). If you do notice an error please take the time - using links at the top or bottom of every page - to let us know.

ISO 1/3 Octave Frequency Bands

The ISO 1/3 Octave Preferred Frequency Table is shown below:

Band No.	Preferred (Hz)	Calculated Center (Hz)	Band Range	Notes
1	1.25	1.26	1.12 - 1.41
2	1.6	1.58	1.41 - 1.78
3	2.0	2.0	1.78 - 2.24
4	2.5	2.51	2.24 - 2.82
5	3.15	3.16	2.82 - 3.55
6	4	3.98	3.55 - 4.4
7	5	5.01	4 - 6
8	6.3	6.31	6 - 7
9	8	7.94	7 - 9
10	10	10.0	9 - 11
11	12.5	12.59	11 - 14
12	16	15.85	14 - 18
13	20	19.95	18 - 22	Start of audible range
14	25	25.12	22 - 28
15	31.5	31.62	28 - 35
16	40	39.81	35 - 45
17	50	50.12	45 - 56
18	63	63.10	56 - 71
19	80	79.43	71 - 90
20	100	100.0	90 - 112
21	125	125.89	112 - 140
22	160	158.49	140 - 179
23	200	199.53	179 - 224
24	250	251.19	224 - 282
25	315	316.23	282 - 353
26	400	398.11	353 - 448
27	500	501.19	448 - 560
28	630	630.96	560 - 706
29	800	794.33	706 - 897
30	1000	1000.0	897 - 1121	Base for ISO Octaves
31	1250	1258.9	1121 - 1401
32	1600	1584.9	1401 - 1794
33	2000	1995.3	1794 - 2242
34	2500	2511.9	2242 - 2803
35	3150	3162.3	2803 - 3531
36	4000	3981.1	3531 - 4484
37	5000	5011.9	4484 - 5605
38	6300	6309.6	5605 - 7062
39	8000	7943.3	7062 - 8908
40	10000	10000	8908 - 11210
41	12500	12589.3	11210 - 14012
42	16000	15848.3	14012 - 17936
43	20000	19952.6	17936 - 22421	Highest Audible

Notes:

Octaves: The blue bands show the start of each ISO Octave. Each Octave is twice the frequency of the previous one.
Base Frequency: Band 30 (1,000 Hz or 1 KHz) is the base frequency for the ISO (and ANSI, BSI etc) Octaves rather than the, perhaps, more obvious 1 Hz starting point. The reason being that frequencies around the 1 KHz range (~400 Hz to ~5 Khz) are more sensitive acoustically and therefore require the greatest accuracy.
Audible Range: The nominal Audible range starts with Band 13 and finishes with Band 43. The audible frequency range is covered by just over 10 Octaves.
Extracting 2/3 Octave Centers: The 2/3 Octave center frequency sequence can be extracted from this table by starting from 1000 Hz and taking every 2nd entry giving a set of Band Numbers of 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42 to cover the audible range. Obviously the band range will have to be re-computed as discussed below (or use this Acoustic Calculator).

Calculating Additional Fractional Octaves: 1/6, 1/12 and 1/24 center frequencies can be derived for this table (or by using this calculator) by applying the formula from any start frequency (Freg):

Freq / 10 ^ (3/(10 * N)) = Center of next lower band OR

Freq * 10 ^ (3/(10 * N)) = Center of next higher band

Where N is the fractional Octave value, for example, 3 for 1/3 Octave, 6 for 1/6 Octave, etc.. Example calculations:

# calculate center of the first 1/3 octave below 1000
Equation: Freq / 10 ^ (3/(10 * N))
Substituting: 1000 / 10 ^ (3/ (10 * 3)) = 794.33
# this places it in the preferred Band 29

# calculate center of next 1/3 octave below band 29
Equation: Freq / 10 ^ (3/(10 * N))
Substituting: 794.33 / 10 ^ (3/ (10 * 3)) = 630.95
# this places it in the preferred Band 28

# calculate center of the first 1/12 octave above 1000
Equation: Freq / 10 ^ (3/(10 * N))
Substituting: 1000 / 10 ^ (3/ (10 * 12)) = 1059.25
# there is no defined Band in the above table (only 1/3 octaves)
# Preferred Frequency is taken from the R40 series (not shown) = 1060

Frequency Band Edges: When using the frequencies defined in this table, ISO 266 states that either the Preferred Center or the Calculated Center may be used depending on the required level of accuracy (where the calculated center is used up to 5 decimal places). The above table, legitimately, uses the Preferred Center value to calculate the band edges. Much of the literature, erroneously, insists on use of the Calculated (or Exact) center. We would argue that for analog purposes and modest digital systems the Preferred Center provides sufficient accuracy. On the other hand precision instruments or advanced digital processing systems should probably use the Calculated Centers. For further discussion on this topic and additional problems arising from this seemingly modest topic, see note 7 of the Fractional Octave Centers Calculator.

Sound Meter Notes

We have just finished coding a sound meter function for our player and audio processing application. It was finally relatively trivial. But reading all the background material was exhausting and ultimately unedifying. These notes capture what we did and the why behind it. They may not be useful for everyone.

There are VU (Volume Unit) meters and Sound meters and Program meters and Peak meters and Peak Program meters.... Most are concerned with measuring a variety of sound sources with much of the literature concerned with standardization - the ability to clearly identify, in a measurable way, an objective value that may be used and understood by multiple parties. Worthy stuff that took us down a number of blind alleys.

We went back to our basic needs rather than get absorbed in purity. Why did we want a meter? What was it going to do? What did we want out of it?

As part of our basic instrumentation of the recorded material we wanted to know something about its playing characteristics. Our ears were telling us how loud it was, but what about the underlying metrics. So we built a meter to this specification. It should probably be called a Peak Sound Meter with Averaging and High-End Density Measure if we were to follow the literature's apparent conventions.

Input: Standard 2 channel, signed 16 bit samples, supporting a range of sample frequencies (8K to 96K in our case).
Channels: Statistics maintained separately for both channels. Since all samples contain both Left and Right the total number of samples processed is kept as a single count.
Averaging: Samples are averaged (currently) over 1/10 second (the display update frequency). When a new sound file is loaded the number of samples in a 1/10 second period is computed (from the sampling frequency) and used as a cut-off/reset and to trigger a display update. Averaging is also provided throughout the sound file (essentially a moving average of all samples to this time) and updated at each trigger point. Many recordings have silence as leaders and trailers and this can detract from the overall usefulness of the moving average feature. It's trivial to eliminate silence at the beginning but distinguishing between silence within the recording (valid effect on average) and silence at the end has so far eluded our modest brains. The positive thing is that trailers are almost universally longer than leaders and thus visually it has little impact. We could always edit the sound file and visually remove the leader/trailer silence if we were feeling particularly energetic or really picky.
Meter Location: Metering occurs when sound is transferred into the systems audio output buffers (we happen to be using PortAudio) both to ensure there is no further sample manipulation and to provide rough visual synchronisation - though there is inevitably some (trivial) latency.
Computation: We compute the RMS (square root (sum of squared samples/number of samples)) for all averaging periods - both the rolling average and our 1/10 second window/display period. We compute the sound power in dBSPL using the Amplitude Ratio equation 20 * log₁₀ (RMS average/MAX_RANGE). MAX_RANGE is 32768 being the highest 16 bit sample value. We use a noise threshold of -60 dbSPL (fairly arbitary) - giving a dynamic range of -60 dBSPL to 0 dBSPL for the meter.
Peak Detection: We check every raw sample for peak - thus we have a single instantaneous peak reading for each channel but currently no method of determining how the peak occurred, for example, was it part of a gradual build-up, an aberrant spike, or simply the maximum value in a sustained loud period. The instantaneous peak is displayed on the meter in dBSPL not as a sample value. The highest dBSPL each 1/10 second window is also captured and is displayed together with the moving average dBSPL.
Sound Intensity: We check every dBSPL sample and if > -12 dBSPL (relatively arbitrary value) we add the count of samples to an intensity counter. We compute the simple percentage as (samples at high intensity/total samples to date * 100) and display on the meter. This figure gives some measure of the loudness intensity of the recorded material.
Statistics: The statistics are maintained for each file in a playlist structure (in our case) and may be interrogated via a menu command at any time.
Meter Display: The meter display is trivial in the extreme. It uses 20 display points (giving 3 dBSPL granularity) and is updated every trigger period (1/10 second). The size of the bar (currently in LED'ish blobs) is calculated by adding 60 to dBSPL and dividing by 3. Values in display points 16/17 (-12 dB SPL to -7 dB SPL) are displayed in yellow, higher values (-6 dBSPL to 0 dBSPL) in red and all lower values in green. The meter bar, moving dBSPL average, peak dBSPL value, instantaneous peak dBSPL and Sound Intensity values are displayed.

Notes:

While it might be obvious (it was not to us until we thought about it), sound meters operate entirely in the Time Domain. Thus, the MAX_RANGE constant has a fairly obvious value of the highest sample value (which occurs in the Time Domain) which, in the case of 16 bit samples, is 32768 (range is +32767 to -32767). Finally, our sound meter runs at the application level and instruments the sound stream as it leaves the player program. It still has to pass through at least one more level of processing (the PC sound controls) before its final passage back to the analog world. We are keenly aware all our measurements relate to the sound file properties and not necessarily the sound perception of the ultimate destination - an ear canal (normally attached to a poor human) since this is affected by real world devices such as amplifiers, loudspeakers and so forth. However, all these influences will be equally applied accross the frequency spectrum and thus the values shown on the meter will be consistently relative to their real-world values, differing only by the gain (in dBSPL) of the subsequent equipment or processes.

A Note on db Scales The term dBSPL defines decibels Sound Pressure Level and is nominally a real-world measure (as measured at the ear canal and with a pressure base of 20 microPascals). As such it appears to have little relevance to the digital world where the term dBFS (decibels Full Scale) is being promoted and which is measured relative to 0 dBSPL. However, in this case to fully describe the passage of sound from a digital source to a human ear would require both the use of the terms dBFS (Full Scale) in the digital domain and dBSPL in the real-world (analog) domain. This may explain why many people opt out of the whole discussion and simply use the term dB which, on its face, is meaningless (dB must always be qualified relative to a base unit of measurement). We continue to use the single term dBSPL since sounds below 0 dB SPL do not exist in the real world (certainly when defined relative to human hearing), thus -dB SPL values can only occur in the digital world and similarly positive dBSPL values can only occur in the real world. In short, no confusion as to the domain can occur when using dBSPL - negative values = digital domain, positive value = real-world domain.
As part of our testing process we calibrated the meter against a -18 db stereo .wav file sample (a 20 second sine wave sample starting and ending on zero). The statistics showed an instant peak of -18 dBSPL (good for the group ego) but the average and peak values were both -21 dBSPL. The sound meter averages over a 1/10 second period and hence, in this case especially, this strategy (used by most meters) does not capture anywhere near the peak. The instant peak capture seems vindicated as the only way any modestly powered instrument can get a measure of the real peak. As a side note, since building the meter, we have been observing just how frequently even relatively stable audio files (showing averages of around -20 to -12 dBSPL and modest, 1 - 5% intensity values, can have (at least one) quite devastating peak of -3 to 0 db typically. Perhaps this may be a one-off aberration within the sound material or perhaps it may be indicative of a pathological audio stream. As noted above, the problem with our current meter strategy is that it does not capture the shape of any peak nor does it even count the number of occurrences. The intensity value gives only a hint of the 'shape' of the file. More work needs to be done on this aspect of the meter if it is to provide meaningful instrumentation.
To summarize our current experience (admittedly very early days) we would say that discussions about VU Meters, Program Meters, Peak Program Meters or any other device that had their history in the analog world may be fascinating (and essential to allow a common base between, say, broadcasting organizations) but in the digital world there is so much more that we can do in terms of instrumenting and analyzing the sound source properties.

A C code sample is shown below for reference only purposes in the hope it might be useful for those experimenting (messing about) in this area. It will not compile free standing. Use at your discretion. Doubtless there are BQF (better, quicker, faster) methods.


// C code sample of peak detecting averaging sound power meter
// - or something like that

// Notes:
// 1. the pointer sbufs points to the METER structure (why sbufs - let's not go there)
//    which is globally available through the current song structure

// base and transients values maintained in METER structure
// the METER structure is globally available for the currently active sound output channel
typedef struct meter_id{
  float      meter_left;                 // sum of left channel samples
  float      meter_right;                // sum of right channel samples
  float      meter_average_left;         // rolling value (reset per song/file)
  float      meter_average_right;        // rolling value (reset per song/file)
  long       meter_total_frames;         // total frames in song
  long       meter_frames;               // no of frames per sample period 
                                         // for this song to give METER_PERIOD time
  long       meter_counter;              // current frames
  long       meter_intensity_left;       // samples > APP_INTENSITY_LEVEL
  long       meter_intensity_right;      // samples > APP_INTENSITY_LEVEL
  int        meter_left_show;            // range -60 to 0 (transient)
  int        meter_right_show;           // range -60 to 0
  int        meter_instant_left;         // instantaneous peak (sample)
  int        meter_instant_right;        // instantaneous peak (sample)
}METER;


// visible and non-transient statistics in SONGSTAT structure
typedef struct songstat_id{
  float      meter_intensity_left_pc;    // percentage intensity
  float      meter_intensity_right_pc;   // percentage intensity
  long       meter_total_frames;         // total frames in song
  int        meter_peak_left_show;       // dbspl peak (-60 to 0)
  int        meter_peak_right_show;      // dbspl peak
  int        meter_instant_left_show;    // instantaneous peak (spl) -60 to 0
  int        meter_instant_right_show;   // instantaneous peak (spl) -60 to 0
  int        meter_average_left_show;    // rolling value range -60 to 0
  int        meter_average_right_show;   // rolling value range -60 to 0
}SONGSTAT;

// the SONGSTAT structure is contained in the SONG * stucture (not shown) 
// - one per song file/stream

// global constants
#define METER_TIME                100               // time in milliseconds for meter averaging
#define METER_PERIOD              (1000/METER_TIME)	// 
#define APP_MAX_SOUND_REFERENCE   32768             // highest 16 bit sample value - create dbSPL
#define APP_INTENSITY_SPL        -12                // dbSPL intensity threshold 
#define METER_DISPLAY_FACTOR      60                // convert to 0 to 60 range
#define APP_METER_GRANULARITY     3                 // current slots per meter
#define APP_METER_FLOOR_DB       -60                // meter display floor -60 dbSPL

// meter_song_start, called when song/stream starts to reset values
// and calculate buffer samples based in samplerate obtained
// from sound file or other source

PRIVATE void meter_song_start(METER * meter, SONG *song)
{
  SONGSTAT *song_stats = song->audiostats; // get song stats reference
	
	// reset meter values
	meter->meter_average_left = 0;
	meter->meter_average_right = 0;
	meter->meter_intensity_left = 0;
	meter->meter_intensity_right = 0;
	meter->meter_left = 0;
	meter->meter_right = 0;
	meter->meter_instant_left = 0;
  meter->meter_instant_right = 0;
	meter->meter_counter = 0;
	meter->meter_total_frames = 0;
	// calculate number of frames in METER_PERIOD based on sample rate
	// of material
	meter->meter_frames = current_song->samplerate/METER_PERIOD);
	
	// reset current song/audio stream values
	song_stats->meter_intensity_right_pc = 0;
	song_stats->meter_intensity_left_pc = 0;
	song_stats->meter_peak_left_show = APP_METER_FLOOR_DB;		// set to low floor
	song_stats->meter_peak_right_show = APP_METER_FLOOR_DB;
	
}

// meter_update (called when sample period counter (meter_frames) reached in callback) 
// calls meter_display function (no wait states since in callback)

PUBLIC void meter_update(METER *meter)
{
  SONGSTAT *this_song = player->song->audiostats; // get song stats reference for current song
	int left_spl, right_spl;
  float right_roll, left_roll;
	float left = sqrt(meter->meter_left / meter->meter_frames); // window RMS
	float right = sqrt(meter->meter_right / meter->meter_frames);
	
	// update rolling average and calculate RMS
	meter->meter_average_right += meter->meter_right;
	meter->meter_average_left += meter->meter_left;
	right_roll = sqrt(meter->meter_average_right / meter->meter_total_frames); average RMS
	left_roll = sqrt(meter->meter_average_left / meter->meter_total_frames);
	
	// convert short window to dbSPL
	meter->meter_left_show = (int)20 * log10(left/APP_MAX_SOUND_REFERENCE);
	meter->meter_right_show = (int)20 * log10(right/APP_MAX_SOUND_REFERENCE);
	
	// convert rolling window to dbSPL and fix floor
	this_song->meter_average_left_show = (int)(20 * log10(left_roll/APP_MAX_SOUND_REFERENCE));
	this_song->meter_average_right_show = (int)(20 * log10(right_roll/APP_MAX_SOUND_REFERENCE));
	if(this_song->meter_average_left_show < APP_METER_FLOOR_DB){
		this_song->meter_average_left_show = APP_METER_FLOOR_DB;
	}
	if(this_song->meter_average_right_show < APP_METER_FLOOR_DB){
		this_song->meter_average_right_show = APP_METER_FLOOR_DB;
	}
	// update SPL peaks and fix floor
	if(meter->meter_left_show < APP_METER_FLOOR_DB){
		meter->meter_left_show = APP_METER_FLOOR_DB;
	}else{
		if (meter->meter_left_show > this_song->meter_peak_left_show){
			this_song->meter_peak_left_show = meter->meter_left_show;
		}
		if (meter->meter_left_show > APP_INTENSITY_SPL){
			meter->meter_intensity_left += meter->meter_counter; // add 'intense' samples
		}
	}
	if(meter->meter_right_show < APP_METER_FLOOR_DB){
		meter->meter_right_show = APP_METER_FLOOR_DB;
	}else{
		if (meter->meter_right_show > this_song->meter_peak_right_show){
			this_song->meter_peak_right_show = meter->meter_right_show;
		}
		if (meter->meter_right_show > APP_INTENSITY_SPL){
			meter->meter_intensity_right += sbufs->meter_counter; // add 'intense' samples
		}
	}

	// to convert for a 20 bar LED display
	// meter->meter_left_show = meter->meter_left_show + METER_DISPLAY_FACTOR / APP_METER_GRANULARITY;
	// meter->meter_right_show = meter->meter_right_show + METER_DISPLAY_FACTOR / APP_METER_GRANULARITY;
	
	// compute percentage intense
	if(meter->meter_intensity_left){
		this_song->meter_intensity_left_pc = ((float)meter->meter_intensity_left / meter->meter_total_frames) * 100;
	}
	if(meter->meter_intensity_right){
		this_song->meter_intensity_right_pc = ((float)meter->meter_intensity_right / meter->meter_total_frames) * 100;	
	}
	// compute instant high sample as dbSPL and fix floor
	this_song->meter_instant_left_show = (int)(20 * log10((sqrt(meter->meter_instant_left * meter->meter_instant_left )/APP_MAX_SOUND_REFERENCE)));
	this_song->meter_instant_right_show = (int)(20 * log10((sqrt(meter->meter_instant_right * meter->meter_instant_right)/APP_MAX_SOUND_REFERENCE)));
	if(this_song->meter_instant_right_show < APP_METER_FLOOR_DB){
		this_song->meter_instant_right_show = APP_METER_FLOOR_DB;
	}
	if(this_song->meter_instant_left_show < APP_METER_FLOOR_DB){
		this_song->meter_instant_left_show = APP_METER_FLOOR_DB;
	}

	meter_display(meter,this_song);
	
	// reset averaging values
	meter->meter_left = 0;
	meter->meter_right = 0;
	meter->meter_counter = 0; // window counter
	
	return;
}

// sound capture snippet in audio callback function
// finds peak and and calculates square root to RMS counters

   // if sound meter active
   long    i,frames;
   int     left,right;
   short   *p = (short *)soundBuffer; // contains normal 16 bit LLRR samples
   frames = framesPerBuffer;        // contains number of frames = LLRR in buffer
			
   for(i = 0; i < frames; i++){
      left = *p++;
      right = *p++;
      if(left != 0){
         // get instant peak
         if(left > meter->meter_instant_left){
            meter->meter_instant_left = left;
         }
         // calculate square for RMS
         meter->meter_left += (float)left * left;
      }
      if(right != 0){
         if(right > meter->meter_instant_right){
            meter->meter_instant_right = right;
         }
         meter->meter_right += (float)right * right;
       }
       meter->meter_total_frames++;
       if(++(sbufs->meter_counter) == sbufs->meter_frames){ // count expired?
          meter_update(meter);  // call meter_update above
       }
    }
			
		// end snippet

FFT Notes

FFT and Frequency Range Interpretation

The Fast Fourier Transform (FFT) is a special case of the Discrete Fourier Transform (DFT). The DFT is used to transform an arbitrary (but finite, hence the Discrete term ) set of samples captured in the time-domain, for example audio data samples, into information about the individual frequency components that comprise the time-domain samples. The frequency components constitute what is called the frequency-domain. Thus, the DFT transforms the time-domain samples into their frequency-domain equivalents. This process may also be reversed. That is, by using an Inverse DFT (and its special case called an Inverse FFT), we can transform from the frequency-domain to the time-domain.

The special case to which the FFT applies is simply where the number of input samples is a power of 2, for example 256, 512, 1024 etc. In this case the time taken to compute the FFT is approximately 100 times less for 1024 samples than for the equivalent DFT calculation and even better at larger samples (order of samples/logbase2(samples)). Not too shabby. While it is technically correct to use the term DFT (the FFT merely being being a special case), in practice FFT has become the dominant term used. The purists don't like it but.... We will follow the well worn path and use the term FFT throughout the following text. If you want to mentally substitute DFT in the appropriate places, feel free to do so.

The FFT algorithm is a strange and wonderful thing for uncovering dark secrets buried in digital time-domain samples. Perhaps not to those who understand the mathematics of it, but to the rest (perhaps majority) of us it most certainly is. It is widely used in all forms of signal processing, audio being but one example. But like all strange and wonderful things it needs infinite care and understanding to yield results and there is....a dark side, things are not always as they seem. The following notes apply solely to the use of the FFT when handling digital audio samples and as such cover a modest subset of the FFT (DFT) power and functionality. The side bar menu gives links to resources that will explain all the gruesome details if you are so inclined.

Note: While much of the data below is based on practical implementation of the FFT using the wonderful FFTW library we have tried, as far as possible to note where FFTW specifics are involved. Consult the documentation for your FFT library, and always - read the fine print.

First some essential background. Numbers may be expressed as real numbers (the normal 1, 2 3 etc. that we use in every day life) or as complex numbers. A complex number has a real (cosine or phase) part and an imaginary (sine or magnitude) part. So what? Digital samples are real, honest to goodness, numbers whose magnitude is determined by the sample size (a.k.a. bit-depth) and which, in music ripped from a CD or captured from a recoding device, and are 16 bits long. The FFT output has slightly different properties when used with real number input values and the next sections only describe this aspect of the FFT. (FFT used with complex numbers are not covered since they are not relevant to sound.)

The FFT assumes as its input that all the samples supplied form a complete, or periodically ocurring, wave comprised of multiple frequencies. When analyzing a stream of data, like music, as a matter of practicality we have to take regular sized chunks (or blocks) of sound samples (such as 1024, 2048, 4096 etc.) from the data stream. The process of handling continuous (or finite but very large) streams of data by dividing it up into regular sized chunks (or blocks) is technically called the Short Time Fourier Transform (STFT). Such chunks (or blocks) have start and end samples that are essentially arbitrary and therefore the entire chunk (or block) cannot, by definition, form a complete wave. The consequence is that the FFT will generate spurious or incorrect frequencies because the sample chunks (or blocks) do not start or end on a wave boundary. To mitigate the effects of the edge conditions we apply a mathematical function (called a window function) to the samples before the FFT. The net result of applying the window function is to taper (or reduce) the size of the two edges. There are a number of window algorithms each of which generates different effects and corresponding artifacts. The most frequently used are rectangular, Hann (typically written as Hanning), Hamming, Bartlett and Blackman. Clearly, the tapering effect of the windowing function when applied to the chunks will lose or mitigate the genuine frequencies which exist in these edge samples. In order to compensate for this effect the samples are overlapped. In essense the effect of overlapping is that new edges are created. Figure 2 shows the effect of windowing and overlapping.

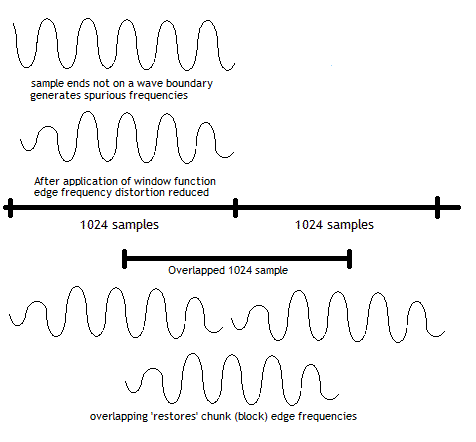
Figure 2 - Windowing and Overlap Effects

Note: There are other reasons to use overlapping.

The FFT algorithm simply takes as input a series (an array) of digital samples (the number of samples are always some power of 2, such as 512, 1024, 2048 and so on) and outputs a corresponding array of complex numbers which represent the magnitude (real part) and the phase (imaginary part) of the frequencies present. Each array element is referred to as a frequency slot or a frequency bin (both terms are widely used and synonymous). So what are the frequencies represented in this output array (slots/bins)? The first position in the output array (element 0) represents a frequency of 0 (which cannot exist and is confusingly referred to as the DC slot (or bin)- see further explanation), the second position (element 1) represents the 1st harmonic (a.k.a fundamental) from which all other frequencies are derived and its frequency width is calculated by the equation 1st (fundamental) harmonic = sample rate/number of samples input. The center point of the slot (or bin) is half this number. Each subsequent position is multiplied by the frequency width to give its ending frequency value. Let's assume that we provide 512 samples to an FFT obtained from file ripped from a CD and whose sample-rate is 44.1KHz (44100 Hz) this gives:

# frequency values of FFT output array
element 0 = represents 0 Hz frequency (the special DC slot)
element 1 = represents 1st (fundamental) harmonic
          = 44100/512 = 86.13 Hz (width)
            (lowest is 0 hz, highest is 86.13 Hz and center = 86.13/2 = 43.06 Hz)
  
element 2 = represents fundamental x 2
          = 86.13 x 2 = 172.26 Hz
            (Lowest is 172.26 - 86.13 Hz = 86.13 Hz, highest is 172.26 
             center = 172.26 - 86.13/2 = 129.2 Hz)
....
element 15 = represents fundamental x 15
           = 86.13 x 15 = 1291.8 Hz (1.298 KHz)
             (lowest is 1291.8 Hz - 86.13 = 1208.67 Hz, highest is 1291.8 
             center = 1291.8 - 86.13/2 = 1248.74 Hz)
and so on

Note: The definitions of highest and center frequencies above are essentially artificial constructs. The FFT calculation is based on the FFT size and thus uses the lowest frequency value. Frequencies which do not fall exactly on these boundaries will result in leakage into adjoining bins. The peak will be in the expected bin but the total power (amplitude) will be spread over the adjacent bins.

The next example assumes 1024 samples input with a sample-rate of 32000 (low/high/center calculations are as above):

# frequency values of FFT output array
element 0 = represents 0 Hz frequency
element 1 = represents 1st (fundamental) harmonic
          = 32000/1024 = 31.25 Hz
element 2 = represents fundamental x 2
          = 31.25 x 2 = 62.5 Hz
....
element 15 = represents fundamental x 15
           = 31.25 x 15 = 468.75 Hz
and so on

Broadly speaking the bigger the number of samples given to the FFT algorithm the finer the granularity of the output frequencies in what are typically called frequency slots or bins (each represented in an output array position or element). Now if we were to continue these calculations to the end of the output array we would get some strange results. Taking our previous example of the 44.1KHz sample-rate with 512 samples would give element 511 (the last element or index) as representing a low frequency of 511 x 86.13 = 44012.43 Hz (44.012 KHz). From sampling (Nyquist) theory we know that the maximum frequency we can obtain is the sample-rate/2 so for 44.1 KHz this gives 22.05 KHz which is represented by element 256 whose high frequency is = 256 x 86.13 = 22049.28 Hz - which is close enough to 22.05 Hz (given rounding errors). This is the so-called Nyquist slot (see explanation). The number of useful elements in the output array when using real values as input is given by the equation number of input samples/2 + 1 (for the insatiably curious the remaining samples represent negative frequencies which for real number inputs are the mirror image - see side bar links for the real scoop).

Note: When operating with only real number input (using the FFTW r2c plan) the FFTW library only outputs N/2 +1 (where N is the number of real input samples) array elements to save on time and space.

The following table shows the granularity of frequency for a number of samples and sample-rates when used with an FFT algorithm (see also the FFT calculator):

Sample Rate	No of Input Samples	Frequency Bins (n/2 +1)	Frequency per bin
96K	512	257 (0 to 256)	187.5 Hz
	1024	513 (0 to 512)	93.75 Hz
48K	512	257 (0 to 256)	93.75 Hz
	1024	513 (0 to 512)	46.87 Hz
44.1K	512	257 (0 to 256)	86.13 Hz
	1024	513 (0 to 512)	43.06 Hz
	2048	1025 (0 to 1024)	21.53 Hz
	4096	2049 (0 to 2048)	10.76 Hz
22.05K	512	257 (0 to 256)	43.06 Hz
	1024	513 (0 to 512)	31.53 Hz
	2048	1025 (0 to 1024)	10.76 Hz
	4096	2049 (0 to 2048)	5.3 Hz
8K	512	257 (0 to 256)	15.62 Hz
	1024	513 (0 to 512)	7.8 Hz
	2048	1025 (0 to 1024)	3.9 Hz
	4096	2049 (0 to 2048)	1.95 Hz

Notes:

The maximum frequency of recorded material on a CD is 20 KHz. Both recording and playback systems use a low pass filter to remove frequencies above this level. The sampling rate of 44.1 KHz is apparently one of those historic artifacts related to magnetic tape recording and the difficulty of designing sharp cut-off filters. The frequency range from 20 KHz (the maximum frequency of a CD) to 22.05 KHz (the theoretical maximum frequency of a 44.1 KHz sample-rate) is effectively dead space.
The frequency range for an FFT is determined by the sampling rate not the source material. A CD is written at a sample rate of 44.1 KHz. If the CD is then read into a PC using a sample-rate of 22.05 KHz then all frequencies above 11.05 KHz are lost. In fact it may be even worse than that. If a low pass filter to remove the frequencies above the sample rate was not used (in the above case to remove anything above 11.05KHz) then these frequencies are still present and when sampled can lead to corruption by sample wrapping or other artifacts (see additional notes).

Handling FFT Output and Input

The following notes may be useful when handling FFT input and output. Recall that in all cases our usage is for processing of digital audio and exclusively (at this stage) 16 bit PCM samples and we use the FFTW library though have looked at many others in our search for FFT nirvana (or something approaching it). In many cases we cover stuff that is well known to those familiar with the topic. We make no apologies for this since we had to discover much of this, with hindsight, trivial stuff by grubbing through the web, reading learned papers which we would, frankly, have preferred not to have read, running copious experiments and wearing out at least three calculators. And that's without mentioning what it did to our modest brains.

Real and Complex Numbers - Part 1: Audio samples, 16-bit, 24 bit or even 32 bit floating point, are real numbers. Most FFT libraries provide options to allow real input to complex output (rather than the traditional complex-in to complex-out) which is ideal for working with digital audio (in the case of FFTW this is fftw_plan_dft_r2c_1d). Where this feature is not provided and the FFT algorithm demands complex number input, simply place the real number in the real part of the complex number and set the imaginary part to zero. Then light the blue touch paper.
FFT Size: The number of samples in the input array (real or complex) are powers of two - some FFT libraries will work with other values but the caveats, and in most cases the run-times, tend to grow alarmingly long. The exact size of the input array (which we call FFT size from here on) is an operational/usage decision and is typically a function of the required frequency granularity (see the FFT and Frequencies discussion) and how the samples are being captured (real time or from a file). Typically sizes will range from 128 (low frequency granularity but fast) to 16384 (great granularity but slow), with 1024, 2048 and 4096 being most common. An FFT size of 2048 samples at a sample rate of 44.1KHz (CD) when trying to provide, say, a real time frequency display represents approximately 1/20 second, meaning that if the output is displayed immediately it will result in a display update of 20 times per second which is probably more than most poor human's eyeballs can handle even if the CPU can. Some form of output averaging technique is probably necessary (more on this topic later).
Channels: This one is probably obvious but let's get it out of the way quickly. Normal audio samples are in 2 channel (stereo) interleaved format (LLRR). These must be separated into left and right hand arrays before being passed to the FFT algorithm. One array consisting only of left hand data will be passed to the FFT and the results obtained, followed by another array with the right hand data. Results from the outputs can be averaged for the two channels if required but never mix the inputs.
Pre-Scaling Input: The FFT algorithm has no idea about your signal. It does not require even to know the sample rate. You stuff numbers in and you get numbers out. If you stuff big numbers in you get big numbers out. 16 bit audio samples are in the range 32767 to -32768. These are big numbers. If you want reasonable numbers out to generate, say a db scale then you will need to normalize in some way either before or after the FFT. The easiest and perhaps most comprehensible solution is to scale the input to the range 1 to -1 by simply dividing by 32768 in the case of 16 bit samples (or 8388608 if using 24 bit samples).
Useful Output:When real numbers are used as input to an FFT then the only useful outputs are an array of N/2 + 1, where N is the FFT size (number of input samples). Thus, if 2048 samples are provided to a real to complex FFT then only 2048/2 + 1 = 1025 array elements are useful, all other values can be ignored or discarded (though this needs to be compensated for in FFT Post Scaling). Indeed, while most FFT algorithms are symmetrical (an array of size n input = an array of size n output, some FFT libraries, notably FFTW, when dealing with real number input only provide an output array of N/2 + 1 size to speed up run-time execution.
Real and Complex - Part 2: The output of an FFT algorithm is an array of complex numbers containing real and imaginary components (some FFT libraries also provide real only outputs). The complex number is itself an array where the real part is the first element [0] and the imaginary part is the second element [1] of each complex number. The following C structure (assuming double is being used, usually both float and long double formats are also provided) illustrates the format.
```
// C99 standard compliant compilers support a complex type by using 
// #include "complex.h"
typedef struct complex_fft{
  double r;			// real (or magnitude) component
  double i;     // imaginary (or phase) component
}FFTRES;
// Alternatively, C99 compliant compilers support a complex type using 
// #include "complex.h"
```
Special Slots (bins): Slot 0 and the Nyquist Slot The FFT returns two unique frequency slots (or bins) which need special treatment: slot 0 (the so-called DC slot) and the N/2 slot (the so-called Nyquist slot). (As a minor aside, watch the flip-flop in all documentation between array size and index value.) The output of the FFT (for real number input FFTs) has a useful size of N/2 + 1 array elements, the array elements have an index value from 0 to N/2. Both special slots (0 and N/2) have a zero imaginary part. That is, only the real part is valid.

Slot 0 (the 0th index) is called the DC component. The real part contains the average of all the input sample values. This slot should be ignored entirely when generating frequency content values for audio applications (there may be application specific reasons to process it for other purposes). Slot (bin) or index 1 is the first valid frequency slot representing a frequency width defined by sample rate/FFT size, which for a sample rate of 44.1KHz and an FFT size of 2048 = 44100/2048 = 21.53 Hz.

Note about the DC slot: The original note above said the DC component (slot/bin 0) has nothing to do with Direct Current. We were wrong in this assertion (thanks to Wiiliam Prescott for pointing out the error of our ways). In fact it has everything to do with Direct Current, however, it is not relevant in audio files (it is always 0) and should be ignored as stated in the text throughout this page. The FFT can be used in many signal processing applications some of these applications, for example, electrical signals, may well have a Direct Current base on which the frequencies to be analysed are superimposed, in which case the DC offset value will be placed in slot/bin 0 (DC has, by definition, 0 frequency, hence the use of slot/bin 0). Audio systems never have a DC component (or rather have a DC component of 0) hence slot/bin 0 can be ignored for these applications.

The real component of the Nyquist slot (index value N/2, where N is the FFT size) contains the magnitude of the signal at the highest valid frequency (defined as sample rate/2). This slot only contains a real part because it describes a sine wave which, since it is the maximum, must start and end at zero and thus has a zero phase (hence the zero imaginary part). Whether it is even included in any frequency display may be a matter of taste or specification. Finally, as previously noted CDs have a low-pass filter on both recording and playback which means there is nothing meaningful at this value when using a sample rate of 44.1KHz (in fact all values above 20K Hz are similarly meaningless).
FFT Post Scaling (and Folding): Read the small print. Most FFT libraries do not normalize the output (though some will take a normalization parameter as input). Simply put this means that you will have to scale all FFT outputs before using them. In the case of FFTW (and most other libraries) this means that you need to scale by the FFT size. So, assuming an FFT size of 2048 samples you need to divide the real and imaginary parts by 2048 before using them in any calculation.

Finally, there are no free lunches. While we defined the useful output array to be N/2 +1 and discarded/ignored the rest these discarded array elements contain 1/2 the real and imaginary values (in mathspeak they are conjugates) for any given frequency slot or bin (slot 0 and the Nyquist slot are ignored). We need to multiply the results (in the real and imaginary parts) by 2 before we use them.

So the full FFT post scale process - performed before using the results - is (ignoring slot 0 and the Nyquist slot) (real part (and imaginary part) * 2)/ FFT size. Phew!
Amplitude: The Amplitude of any frequency slot (or bin, see discussion) is calculated using the equation Amplitude = square root (real part ^ 2 + imaginary part ^ 2). To convert this to dbSPL (a.k.a dbFS) use the equation 20 * log₁₀ (Amplitude). Alternatively, if the db calculation is always going to be performed without the need for the real Amplitude then use Intermediate Amplitude = (real part ^ 2 + imaginary part ^ 2) (without square root) followed by 10 * log₁₀ (Intermediate Amplitude). Note: The real and imaginary parts are assumed to have been post-scaled as required before performing this calculation.
Phase: To calculate the Phase of the frequency slot (or bin) use the equation Inverse Tangent (Imaginary part/Real part) (Inverse Tangent a.k.a arctangent or atan). Again, the real and imaginary parts are assumed to have been post-scaled as required before performing this calculation.
Dynamic Range/Noise Floor: The FFT process is full of mysteries. When you start getting some figures in dbSPL they can look more than a tad weird. In particular you expect silence (all zero input) to be -96 dbSPL (the dynamic range of a 16 bit sample is 0 to -96 db using the simplistic rule of thumb of 6 db per bit). When you play silence you may be seeing well in excess of this value -120 db or even higher. The FFT pushes down the noise floor (or increases the dynamic range) by a factor of 10 * log₁₀(fft size/2). So for an FFT size of 2048 this adds ~30 db, giving a noise floor for silence of -126 db.
Calibration: This stuff is not simple. And the really interesting question is: when you think your results are correct how can you prove it? Running any old crummy .mp3 or even a .wav file of your favorite music is going to generate more questions than answers. Unless, of course, you know that at 23.77 seconds the value of the frequency 1.2K is -27 db. The only way is to use known input. If you search the web there are plenty of test files (mostly, and for obvious reasons, in either .wav or .aiff format) that can be used to calibrate your code. To use anything else is to spend hours and days playing with the problem. If you really want some fun, try both normal sine wave samples and some equivalent square wave samples.
Undersampled Audio Material: We have some audio material with sample rates of 22.05, 11.025 and even 8KHz whose provenance and history we do not know. When we run this material through our frequency analysis (fully calibrated!) we get lunatic lows of -140 to -150 db SPL. There are two possible explanations for this phenomenon. First, (and most likely) is that the original material did contain frequencies above the sampling rate and a low-pass filter was not used to remove them. In this case, assume we are sampling at 22.05K (giving a maximum frequency of 11.025 KHz) and a signal with a value of 13K is detected. Depending on the ADC being used and its surrounding circuitry the generated sample may well be wrapped since it is beyond the scope of the ADC. While the resulting audio stream will play (normally surprisingly well) because playing only uses the time-domain. However, when subjected to FFT analysis this undersampling/wrapping phenomenon manifests itself as essentially aberrant values. The second possibility is that, in an attempt to improve the quality of the digital audio material, the file has previously been equalized and DSP'd beyond valid limits resulting again in a file which when subject to FFT analysis manifests the aberrant effects (but still plays).
Frequency Spread (Leakage): The FFT (in reality the DFT) has all kinds of necessary limitations. When a frequency is present but is not exactly on a bin boundary (defined as any multiple of sample rate/FFT Size) then the frequency power is spread over the adjacent bins. The further the frequency is from the bin border the more leakage occurs. Increasing the FFT size will ameliorate the leakage (because the bin widths are smaller the frequency will get closer to a bin boundary) but, unless it is exactly on the boundary (impossible with, essentially, random frequency music files) will not eliminate it. The peak can be tightened (reducing the spread) with a windowing function but this reduces the peak power of the signal even further. Looks like we may have to read more learned papers. Sigh.
Average and Peak Output: Depending on the application, the FFT output may be, in the words of the quaint New York expression, "like drinking from a fire-hydrant". In other words a little too much of a good thing. For example, in a real-time frequency analysis display you may want to show the results of the left and right channels on a single display or if your FFT size is 2048 (representing 1/20 second at 44.1K) but you may only want to update the display 4 times a second. In both cases you have one of two possible strategies. Show the peak or the average. Both are legitimate and frequently used techniques. In all cases the work should be done with the FFT post scaled output and will depend on precisely what you are displaying. In the case of a db display this means working with the calculated amplitude. When measuring the peak, simply save the output and compare it with all subsequent values in the selected time range, replacing it with a subsequent value if higher. In the case of averaging this should be done as the Root Mean Squared (RMS) not the simple mean (RMS is calculated as sqrt(amplitude 1 ^2 + amplitude 2 ^2...amplitude n ^2/number of values)).

FFT Windows, Leakage and Over-Lapping

Placeholder - details to be supplied.

Inverse FFT

There is simply no end to the magic of the FFT. By taking an array of complex numbers representing the various frequencies the FFT can be used to construct an array of time-domain samples!

Placeholder - details to be supplied.

FFTW Notes for Windows 7 and VS Express 2008

Some Notes on working with FFTW in a Visual Studio 2008 Express Edition.

The FFTW documentation notes in the README-WINDOWS file that the LIB command must be run to generate the required .lib file for MS Linking when working with DLLs. In order to ensure that the correct environment is set up this should be done when the current project is loaded using the VS Command Line Tool (Tools->Visual Studio 2008 Command Prompt and run lib /def:full/path/to/def/file /out:full/path/of/required/lib/file. Simply running the lib command from an ordinary command prompt will not work. As a passing note FFTW provides both 32 bit and 64 bit versions of the DLLs and it is possible to use the 64 bit versions even when building a Win32 solution.

Problems, comments, suggestions, corrections (including broken links) or something to add? Please take the time from a busy life to 'mail us' (at top of screen), the webmaster (below) or info-support at zytrax. You will have a warm inner glow for the rest of the day.